Li, S., Liu, M., Hanoar, D., Gan, Y. (2018) Dynamics of Viscous Entrapped Saturated Zones in Partially Wetted Porous Media. Transport in Porous Media. In press. [DOI]
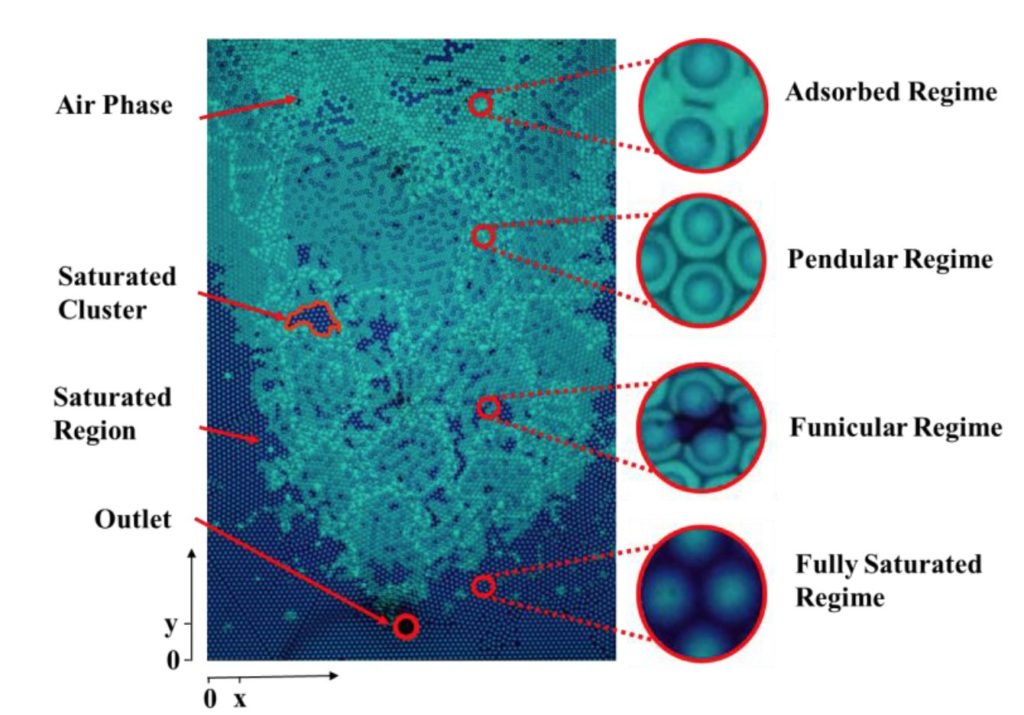
As a typical multiphase fluid flow process, drainage in porous media is of fundamental interest both in nature and in industrial applications. During drainage processes in unsaturated soils and porous media in general, saturated regions, or clusters, in which a liquid phase fully occupies the pore space between solid grains, affect the relative permeability and effective stress of the system. Here, we experimentally study drainage processes in unsaturated granular media as a model porous system. The distribution of saturated clusters is analysed by optical imaging under different drainage conditions, with pore-scale information from Voronoi and Delaunay tessellation used to characterise the topology of saturated cluster distributions. By employing statistical analyses, we describe the observed spatial and temporal evolution of multiphase flow and fluid entrapment in granular media. Results indicate that the distributions of both the crystallised cell size and pore size are positively correlated to the spatial and temporal distribution of saturated cluster sizes. The saturated cluster size is found to follow a lognormal distribution, in which the generalised Bond number (Bo∗) correlates negatively to the scale parameter (μ) and positively to the shape parameter (σ). With further consideration of the total surface energy obtained based on liquid–air interfaces, we were able to include additional grain-scale information in the constitutive modelling of unsaturated soils using both the degree of saturation and generalised Bond number. These findings can be used to connect pore-scale behaviour with overall hydro-mechanical characteristics in granular systems.
Full paper can be downloaded via Publications page.
Leave a Reply